4.5 Properties of Estimators
SW 2.5, 3.1
Suppose we are interested in some population parameter \(\theta\) — we’ll write this pretty generically now, but it could be \(\mathbb{E}[Y]\) or \(\mathbb{E}[Y|X]\) or really any other population quantity that you’d like to estimate.
Also, suppose that we have access to a random sample of size \(n\) and we have some estimate of \(\theta\) that we’ll call \(\hat{\theta}\).
As before, we are going to consider the repeated sampling thought experiment where we imagine that we could repeatedly obtain new samples of size \(n\) and with each new sample calculate a new \(\hat{\theta}\). Under this thought experiment, \(\hat{\theta}\) would have a sampling distribution. One possibility for what it could look like is the following
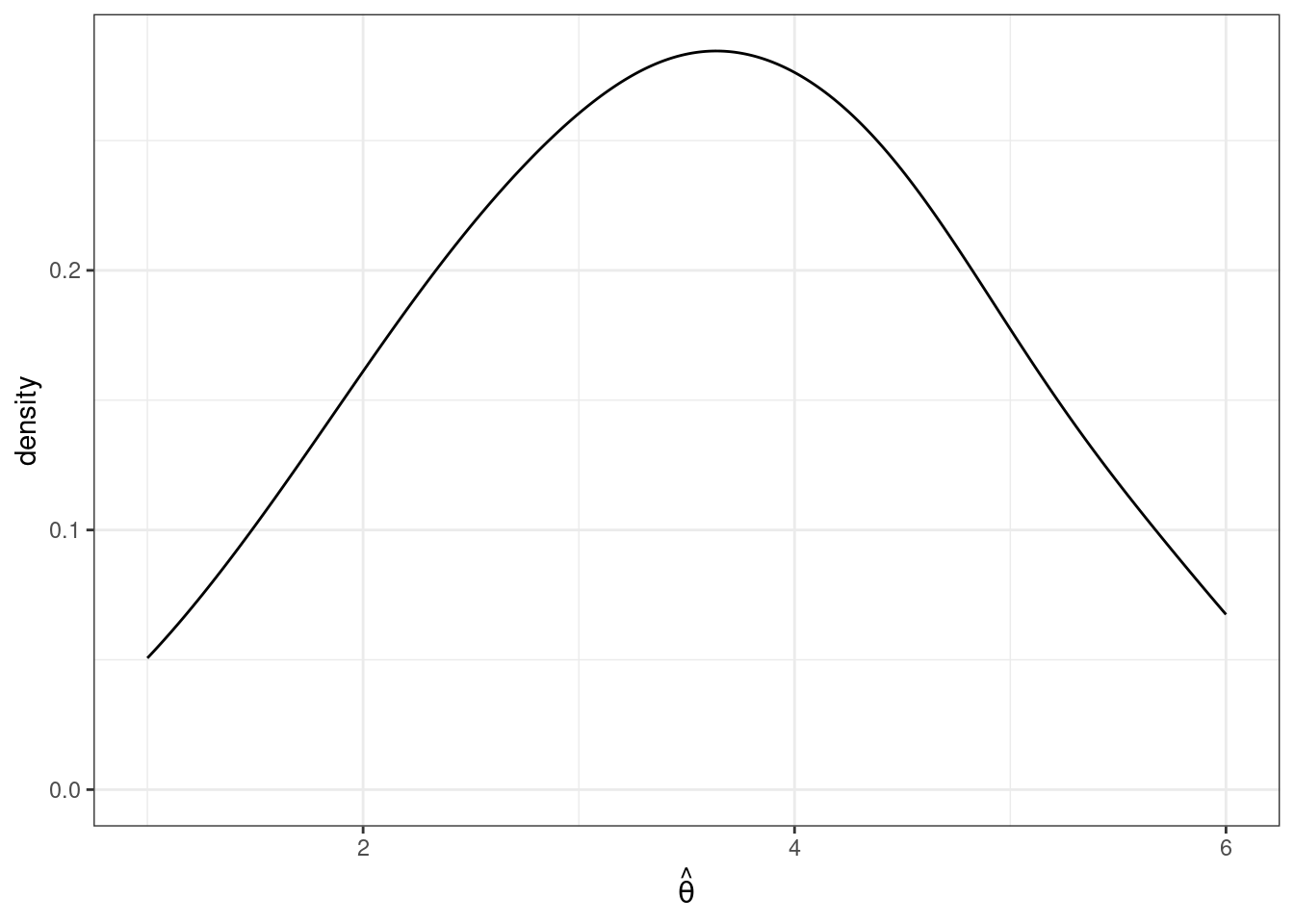
In this case, values of \(\hat{\theta}\) are more common around 3 and 4, but it is not highly unusual to get a value of \(\hat{\theta}\) that is around 1 or 2 or 5 or 6 either.
The first property of an estimator that we will take about is called unbiasedness. An estimator \(\hat{\theta}\) is said to be unbiased if \(\mathbb{E}[\hat{\theta}] = \theta\). Alternatively, we can define the bias of an estimator as
\[ \textrm{Bias}(\hat{\theta}) = \mathbb{E}[\hat{\theta}] - \theta \] For example, if \(\textrm{Bias}(\hat{\theta}) > 0\), it means that, on average (in the repeated sampling thought experiment), our estimates of \(\theta\) would be greater than the actual value of \(\theta\).
In general, unbiasedness is a good property for an estimator to have. That being said, we can come up with examples of not-very-good unbiased estimators and good biased estimators, but all-else-equal, it is better for an estimator to be unbiased.
The next property of estimators that we will talk about is their sampling variance. This is just \(\mathrm{var}(\hat{\theta})\). In general, we would like estimators with low (or 0) bias and low sampling variance. Let me give an example
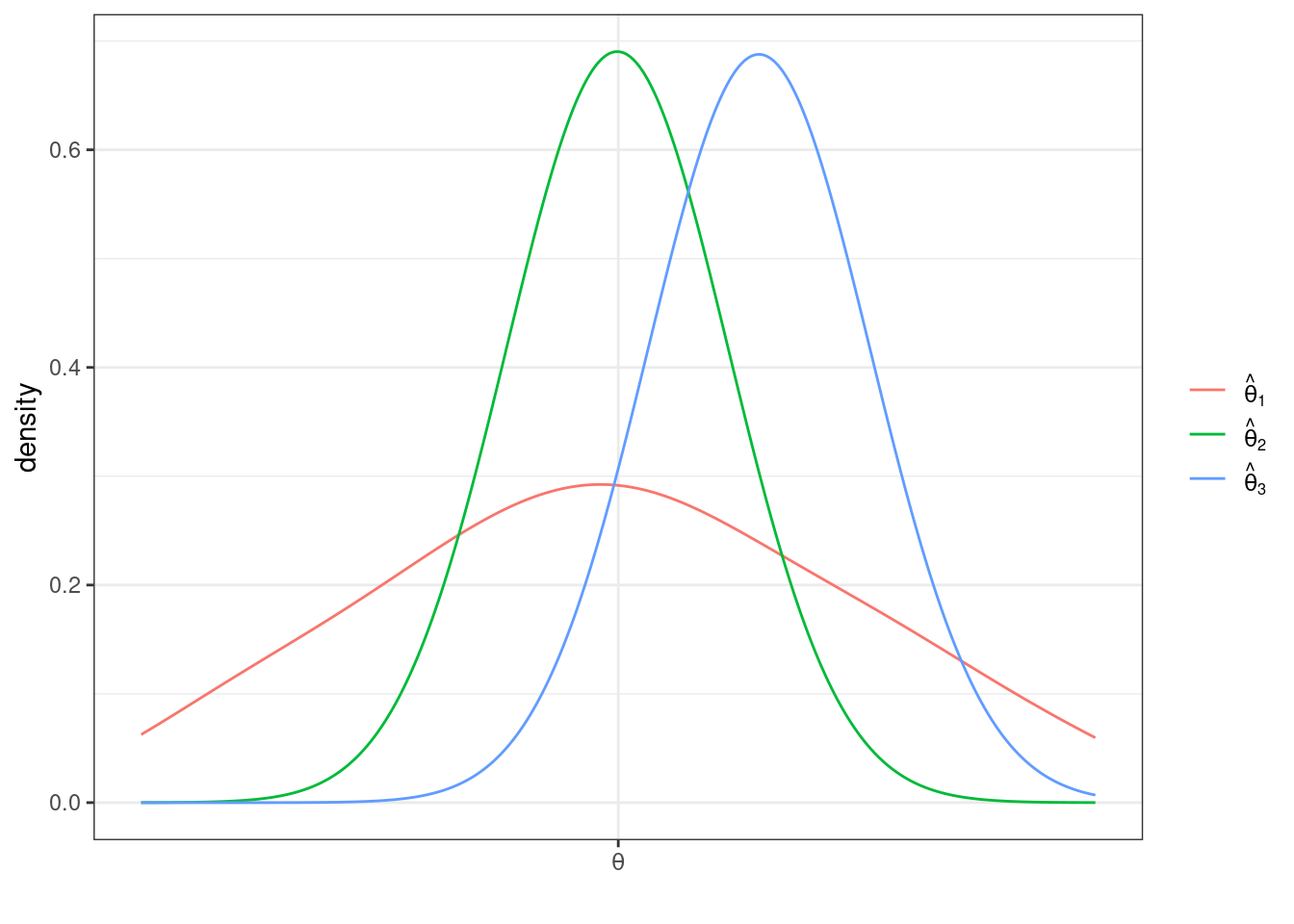
This is a helpful figure for thinking about the properties of estimators. In this case, \(\hat{\theta}_1\) and \(\hat{\theta}_2\) are both unbiased (because their means are \(\theta\)) while \(\hat{\theta}_3\) is biased — it’s mean is greater than \(\theta\). On the other hand the sampling variance of \(\hat{\theta}_2\) and \(\hat{\theta}_3\) are about the same and both substantially smaller than for \(\hat{\theta}_1\). Clearly, \(\hat{\theta}_2\) is the best estimator of \(\theta\) out of the three. But which is the second best? It is not clear. \(\hat{\theta}_3\) systematically over-estimates \(\theta\), but since the variance is relatively small, the misses are systematic but tend to be relatively small. On the other hand, \(\hat{\theta}_1\) is, on average, equal to \(\theta\), but sometimes the estimate of \(\theta\) could be quite poor due to the large sampling variance.