Five Minute Summary: Policy Evaluation during a Pandemic
Introduction
Tong Li and I just posted a new working paper called Policy Evaluation during a Pandemic. This is our second paper about policy evaluation in the context of the pandemic. In the first paper, Evaluating Policies Early in a Pandemic: Bounding Policy Effects with Nonrandomly Missing Data, we were mainly interested in dealing with Covid-19 testing being non-random (as well as different testing rates, etc. across different locations). In that paper, we ended up proposed a matching estimator, but we got a lot of comments asking: Why not difference-in-differences?
We became quite interested in answering that question. Originally, we just “had the sense” that DID was not the right tool to use here. But that has developed into a fully fledged paper now.
And our answer turns out to be the same as before: to us, it seems like a lot better idea to carefully condition on pre-treatment pandemic related variables (e.g., number of cases, fraction of the population still susceptible, population size, and perhaps other variables like population density or demographics) rather than try to “difference out” location-specific fixed effects. In other words, we think unconfoundedness-type identification strategies are likely to be more appropriate than DID-type identification strategies when it comes to identifying effects of Covid-19 related policies.
DID or Unconfoundedness for Evaluating Policies during a Pandemic?
The key issue is that epidemic models from the epidemiology literature are highly nonlinear. A leading example is stochastic SIRD model (SIRD stands for S=Susceptible, I=Infected, R=Recovered, D=Dead). The key equations in this model look like
\[I_{lt}(0) = (1-\lambda-\gamma)I_{lt-1}(0) + \beta \frac{I_{lt-1}(0)}{N_l} S_{lt-1}(0) + U_{lt}\]where \(\lambda, \gamma,\) and \(\beta\) are parameters related to the recovery rate, death rate, and infection rate, respectively; \(N_l\) is the number of individuals in a particular location, \(U_{lt}\) is an idiosyncratic shock, and variables indexed by \(\bullet(0)\) are “potential outcomes” (the values those variables would take if the policy were not implemented).
You can immediately see that this is a much different model from the one that would typically lead to difference in differences:
\[I_{lt}(0) = \theta_t + \eta_i + U_{lt}\]where \(\theta_t\) is a time fixed effect and \(\eta_i\) is an individual fixed effect.
This shouldn’t be a big surprise either — pandemics are much different from many of the panel data sorts of applications that we commonly consider in economics. In particular, the spread of a pandemic is not really related to a particular location’s “pandemic fixed effect”; this is much different from, say, applications in labor economics where it seems much more reasonable to think that an individual’s earnings are related to their unobserved, time invariant “skill”.
Does the identification strategy actually matter?
The short answer is: yes.
In the paper we consider both simulations related to this and an application on shelter-in-place orders. Just to keep things short, let’s just consider the simulations here.
For the simulations, for simplicity, we consider the case where the policy has no effect on Covid-19 cases (this makes it easy to check if the approach is working well as we can just check if estimated policy effects are close to 0). In addition, we consider the case where the first Covid-19 case tends to show up in treated locations earlier than for untreated locations.
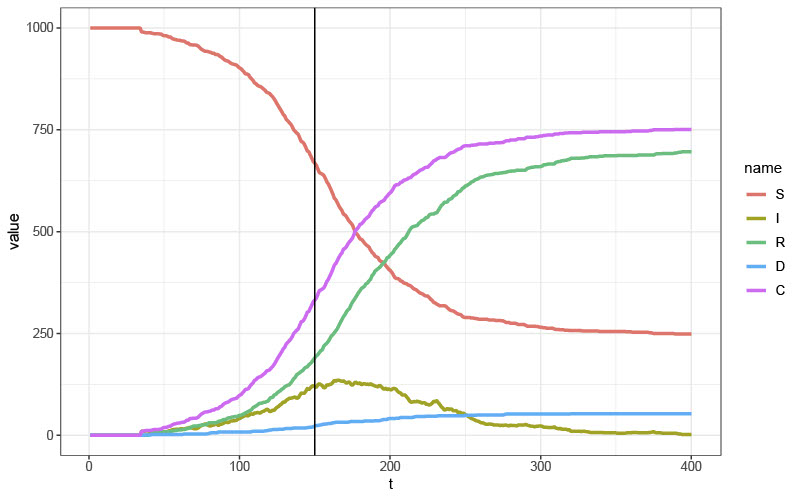
To start with, here is a plot of what a pandemic looks like in a stochastic SIRD model. The notation here is the same as above; the additional variable \(C\) is the cumulative number of cases. The policy is implemented when \(t=150\), but it has no effect.
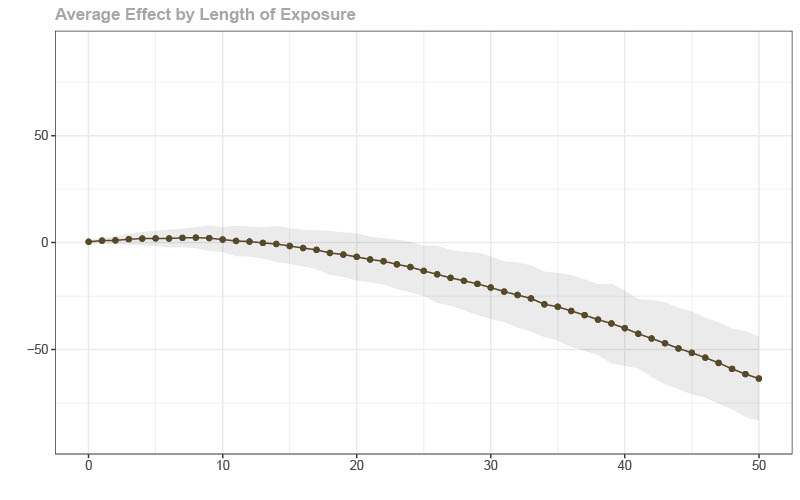
Next, is a figure showing estimated effects of the policy on cumulative Covid-19 cases using DID. Here, we (incorrectly) estimate that the policy decreased cumulative cases. Basically, treated locations (which tended to get their first cases earlier) and untreated locations are not following the same path of untreated potential outcomes due to the nonlinearity of the model. Interestingly, it is possible to make the bias positive if you set the timing of the policy differently.
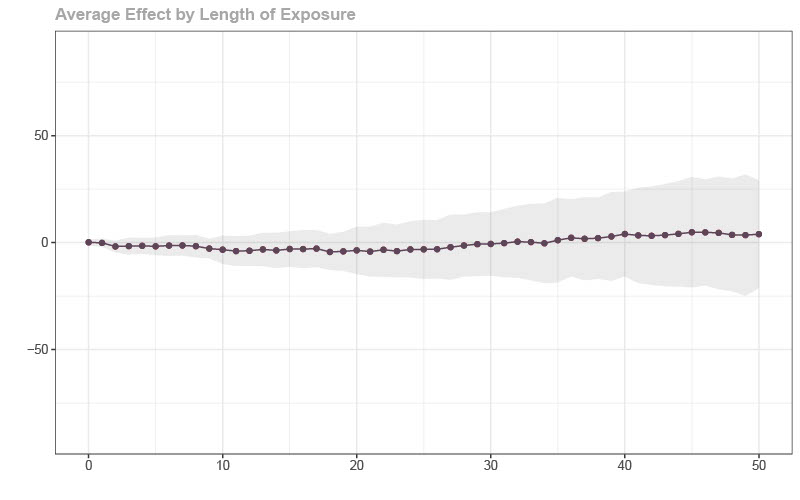
The last figure involves estimating the effect of the policy by comparing locations that have similar pre-treatment pandemic-related characteristics (i.e., under unconfoundedness as we suggest doing in the paper). You can immediately see that this approach works much better.
The Rest of the Paper…
-
We propose doubly robust estimators of policy effects. These sorts of estimators are attractive in this case because they provide consistent estimates of policy effects if either (i) the propensity score (which is related to modeling the probability that a location adopts the policy) or (ii) an outcome regression model (related to the epidemic model in the absence of the treatment) is correctly specified. This setup is very attractive here as it gives a way to evaluate policies while partially circumventing the challenge of estimating a full pandemic model. Basically, we get to the case where you need to compare locations that implemented the policy to locations that didn’t implement the policy (or implemented it later) conditional on having the same pre-policy characteristics that are related to the pandemic — economists know a lot about this setting.
-
We also consider the case where a researcher is interested in understanding the effect of a Covid-19 related policy on an economic outcome (rather than Covid-19 cases) in the particular case when (i) the policy can affect the outcome directly, (ii) the policy can affect the number of Covid-19 cases, and (iii) the number of Covid-19 cases can have its own effect on the economic outcome. We show:
-
Neither standard DID nor including number of cases as a covariate deliver consistent estimates of ATT-type parameters in this case.
-
We propose a way to “adjust” for the policy affecting cases and deliver a reasonable ATT-type effect of the policy on economic outcomes.
-
-
We also have an application about the effects of shelter-in-place orders on Covid-19 cases and recreational travel. We find that the results are quite sensitive to which methodological approach one chooses.